Matematicas

"LA IMPORTANCIA DEL AGUA PARA LA VIDA" "THE IMPORTANCE OF WATER FOR LIFE"

Es esencial tomar acciones concretas y efectivas para un uso responsable del agua dulce potable teniendo al ahorro a un consumo solidario y evitar el derroche de este recurso natural  vital para la vida en nuestro planeta.
It is essential to take concrete and effective actions for the responsible use of fresh drinking water, saving money to support consumption and avoiding the waste of this natural resource vital for life on our planet.

La importancia 

 del agua es muy importante

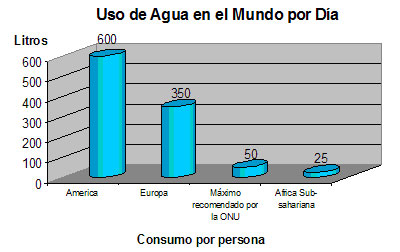
 para todos los seres vivos del planeta, ya que es el elemento que necesitan en todo el mundo. Pero en cambio, el ser humano busca este rico elemento en perjuicio de su propia especie y perjuicio de su propia vida y existencia como la del resto de los habitantes de la tierra ya sea por animales, plantas y por supuesto los humanos. Se dice que el ser humano puede llegar a necesitar 

hasta 500 litros de agua potable.

The importance of water is very important for all the living beings of the planet, since it is the element that they need in the whole world. But instead, the human being seeks this rich element to the detriment of their own species and damage their own life and existence as the rest of the inhabitants of the earth either by animals, plants and of course humans. It is said that the human being may need toup to 500 liters of drinking water.

 Resulta que el 70% de la tierra sea agua y que el 70% de nuestro cuerpo sea agua. Lo más recomendable para tener una dieta saludable y una larga vida, es comer alimentos con un porcentaje del 70% en agua para poder desarrollar nuestro cuerpo muy

sanamente.

It turns out that 70% of the earth is water and that 70% of our body is water. The most advisable to have a healthy diet and a long life, is to eat foods with a 70% percentage in water to be able to develop our body very healthily.

Fuera del mar, el agua potable es apenas solo un 1% de todo el agua existente, el 96% restante es agua salada que se encuentra en los mares, y el 3% que falta es el agua que se encuentra en los polos en forma

de hielo. Y aunque parezca que llueve a menudo  y que disponemos de forma muy gratuita e ilimitada

del agua, es todo lo contrario. La tierra cada vez se encuentra caliente, el aumento de habitantes va creciendo en las zonas donde se contemplaban ecosistemas hermosos donde antes cultivaban sus alimentos , pero ahora se esta convirtiendo en el principal problema de hambre a nivel mundial.

Outside the sea, drinking water is only 1% of all existing water, the remaining 96% is salt water that is found in the seas and the 3% that is missing is the water that is in the poles of ice. And although it seems that it rains often and that we have very free and unlimited. Of water, it is the opposite. The earth is getting warmer, the increase of inhabitants is growing in the areas where beautiful ecosystems were contemplated where previously they cultivated their food, but now it is becoming the main problem of hunger in the whole world.

"CONSUMO RESPONSABLE DEL AGUA" RESPONSIBLE WATER CONSUMPTION.

El agua participa, de forma directa e indirecta, en todos los procesos de producción. En muchas actividades económicas del sector primario la cantidad de agua disponible determina el tipo, la cantidad y la cantidad de productos obtenidos (agricultura, ganadería, entre otras.

Water participates, directly and indirectly, in all production processes. In many economic activities of the primary sector, the amount of water available determines the type, quantity and quantity of products obtained (agriculture, livestock, among others).

En el sector secundario, el agua se utiliza como refrigerante de alimentos y en las tareas de limpieza.

In the secondary sector, water is used as a food coolant and in cleaning tasks.

El sector terciario se relaciona con todo el tipo de servicios para hacer posibles algunos procesos de transformación de los productos.

The tertiary sector is related to all kinds of services to enable some processes of product transformation.

El crecimiento de la población, la contaminación o destrucción de fuentes naturales de agua limpia y el mal uso que le hemos dado, estan poniendo en peligro al agua del planeta.

The growth of the population, the contamination or destruction of natural sources of clean water and the misuse we have given it, are endangering the water of the planet.

  A continuación se presentan algunas medidas de preventivas para evitar el desaprovechamiento del agua potable,  para cuidar de ella y cuidar a todos los seres vivos que la necesitan y para los que la habitan en los mares:

Below are some preventive measures to avoid wasting drinking water, take care of it and take care of all the living beings that need it and those who inhabit it in the seas:

Resultados de la Web

Resultados de la 

• Una canilla que gotea por segundo, acaba gastando 30 litros de agua por día. Si vez una canilla goteando, no seas perezoso: ¡Ciérrala! .  A tap that drips per second, ends up spending 30 liters of water per day. If you see a faucet dripping, do not be lazy: Close it!

• Cierra la llave del lavabo mientras te enjabonas las manos, te afeitas o te lavas los dientes. Una canilla abierta consume hasta 12 litros por minuto; puedes llegar a ahorrar ¡20 litros de agua por vez!. Close the sink key while you lather your hands, shave or brush your teeth. An open tap consumes up to 12 liters per minute; You can save 20 liters of water at a time!

• Al ahorrar agua caliente, no solo ahorrarás agua sino energía. By saving hot water, you will not only save water but energy.

• El agua NO potable puedes usar para regar las plantas del jardín. Non-drinking water can be used to water the garden plants.

• Al ducharte, mientras te enjabonas o te colocas el shampoo, cierra la ducha y así ahorrarás casi 10 litros. When showering, while you soap yourself or put the shampoo, close the shower and thus save almost 10 liters.

• No uses el inodoro como basurero, tira de la cadena cuando solo sea necesario. Do not use the toilet as a garbage can, pull the chain when it is only necessary.

• Usa cubetas con agua o trapos húmedos para lavar el auto, en vez de mangueras. Use buckets with water or damp rags to wash the car, instead of hoses.

• Aprovecha la lluvia para regar tus plantas, no vuelvas a regar si es que ya llovió. Take advantage of the rain to water your plants, do not water again if it has already rained.

• Usa la ducha en vez de la tina o canilla para bañarte. Use the shower instead of the tub or tap to bathe.

Por lo tanto estos consejos nos ayudarán a evitar el desperdicio de agua potable y para cuidar de ella, ya que es el elemento que necesitamos para sobrevivir.
Therefore, these tips will help us to avoid wasting drinking water and to take care of it, since it is the element we need to survive.

"¿De dónde proviene el agua que consumimos?" Where does the water we consume come from?

El agua que actualmente ocupamos en el hogar para usos de aseo personal o para la cocina proviene de un nacimiento que se encuentra ubicada en Jalacingo Veracruz, ya que en ése lugar se encuentra un hermosa presa donde hay tubos que absorben el agua de la presa para poder trasladarla hasta nuestro hogar, por lo que pasa un largo tiempo para poder llegar.
The water that we currently occupy in the home for personal hygiene or kitchen uses comes from a birth that is located in Jalacingo Veracruz, since in that place there is a beautiful dam where there are pipes that absorb water from the dam. We can move it to our home, so it takes a long time to get there.

El agua recorre un buen tramo desde su punto de inicio hasta nuestro hogar, ya que pasa por diferentes municipios, por lo que tarda un poco hasta poder llegar a nuestro hogar. Aproximadamente el agua recorre un promedio de  4-7 km desde su punto de inicio hasta nuestro hogar, por lo que a veces tarda un poco para llegar.
 The water travels a good stretch from its starting point to our home, as it passes through different municipalities, so it takes a while to get to our home. Approximately the water travels an average of 4-7 km from its starting point to our home, so sometimes it takes a while to get there.


A continuación les presento un croquis en un plano cartesiano donde podrán observar el recorrido que utliza el agua hasta nuestro hogar por algunos puntos importantes:
Then I present a sketch on a Cartesian map where you can see the route used by the water to our home by some important points:

Como puedes observar en el croquis hay diferentes puntos en el plano cartesiano, ya que en esos puntos hay diferentes lugares donde pasa el agua potable desde Jalacingo hasta nuestro hogar. Por lo que  a  continuación les voy a dar a conocer en que coordenadas se encuentran esos puntos:
As you can see in the sketch, there are different points in the Cartesian plane, since in those points there are different places where drinking water passes from Jalacingo to our house. For what then I will let you know in what coordinates these points are:

*El origen del agua se encuentra en (5.5, -9). The origin of the water is in (5.5, -9).

*La panadería Claudia se encuentra en (4.5, -4). The Claudia bakery is in (4.5, -4).

4

*La pollería se encuentra en (1.3, -1). The poultry shop is in (1.3, -1).

*La tienda Maria se encuentra en (-0.2, 0.4). The Maria store is located at (-0.2, 0.4).

*La tienda de abarrotes se encuentra en (1, -5.4). The grocery store is located at (1, -5.4).

*El taller se encuentra en (5.5, 3).The workshop is in (5.5, 3).

*La tienda Marta se encuentra en (-2.4, 3.5). The Marta store is in (-2.4, 3.5).

*La iglesia se encuentra en (-5, -3.1). The church is located at (-5, -3.1).

*La clínica se encuentra en (-6.2, 2). The clinic is in (-6.2, 2).

*Y por ultimo mi hogar se encuentra en las coordenadas de (-7.5, 7). And finally my home is at the coordinates of (-7.5, 7).

Las personas siempre se lavan las manos cada vez al comer un alimento, ya que la mano tiene muchas bacterias que nos provocan enfermedades en el estómago. Yo comunmente me lavo las manos de 3-5 veces, ya que siempre me las lavo cada vez que voy a ingerir algún alimento.

Por lo que a continuación les presento una tabla en donde podrán observar las veces que me lavo la mano y la cantidad de agua que utilizo: 

People always wash their hands every time they eat a food, since the hand has many bacteria that cause stomach diseases. I commonly wash my hands 3-5 times, since I always wash them every time I go to eat some food.
So then I present a table where you can see the times I wash my hand and the amount of water I use:

Lavar las manos			Formula de litros  1x=?
veces	1	2	3	4	5
Litros utilizados	1(1)=1	1(2)=2	1(3)=3	1(4)=4	1(5)=5

En mi casa somo un total de 8 integrantes , por lo aveces vamos 6 veces al baño, pero hay días donde vamos aproximadamente más veces al baño.

Por lo que lo que aveces gastamos mucha agua, ya que el inodoro le caben 6 litros aproximadamente, por lo que debemos de gastar menos agua. 

In my house we are a total of 8 members, so sometimes we go to the bathroom 6 times, but there are days where we go approximately more times to the bathroom.
So what we sometimes spend a lot of water, since the toilet will fit about 6 liters, so we must spend less water.

Al igual utilizo agua al bañarme, ya que es importante bañarnos diariamente para no padecer infecciones por higiene. Aproximadamente yo utilizo 19 litros de agua al bañarme para quitarme la suciedad que adquiero durante el dia . Por lo que a continuación les presento una pequeña tabla donde podrán observar la cantidad de litros que utilizo todos los días:

I also use water when bathing, as it is important to bathe every day so as not to suffer from hygiene infections. Approximately I use 19 liters of water when bathing to remove the dirt that I acquire during the day. So below I present a small table where you can see the amount of liters I use every day:

Tomar una ducha			Formula de litros  19x=?
veces	1	2	3	4	5	6	7
Litros utilizados	19(1)=19	19(2)=38	19(3)=57	19(4)=76	19(5)=95	19(6)=114	19(7)=133

En mi hogar siempre ensuciamos trastes, por lo que siempre los tenemos que lavar para volverlos a utilizarlos cada vez que ingerimos un alimento, por lo que utilizamos aproximadamente la cantidad de 15 litros para lavar los trastes y para estar limpios. A  continuación les presento una tabla donde observaran la cantidad de agua que utilizamos cada vez que lavamos los trastes todos los días: 

In my home we always dirty frets, so we always have to wash them to use them again every time we eat a food, so we use approximately 15 liters to wash the dishes and to be clean. Then I present a table where you will see the amount of water we use every time we wash the dishes every day:

Lavar los trastes			Formula de litros utilizados  15x=?						Total:
días	1	2		3	4	5	6	7	7
Litros utilizados	15(1)=15	15(2)=30		15(3)=45	15(4)=60	15(5)=75	15(6)=90	15(7)=105	105 litros a la semana

Y por ultimo les presento una tabla donde observaran la cantidad de veces que utilizamos el inodoro y la cantidad de litros que utilizamos:
And finally I present a table where you will see the number of times we use the toilet and the number of liters we use:

Inodoro				Función de litros  6x=?
Descarga	1	2	3		4	5	6
Litros	6(1)=6	6(2)=12	6(3)=18		6(4)=24	6(5)=30	6(6)=36

"Sugerencias" Suggestions.

* Reutiliza el agua de las lluvias para ahorrar agua.
Reuse rainwater to save water.

* No dejes el grifo abierto al lavarte los dientes o afeitarte.
Do not leave the tap open when brushing your teeth or shaving.

* No mantengas el grifo abierto al fregar los platos.
Do not keep the tap open when doing the dishes.

* Revisar si hay fugas en el baño o la cocina.
Check for leaks in the bathroom or kitchen.

* Usa cubetas con agua o trapos húmedos para lavar el auto, en vez de mangueras. Use buckets with water or damp rags to wash the car, instead of hoses.

SITUACIÓN 2

"Mis hechos... Y desechos"

¿Qué significa basura?

Como basura denominamos a cualquier desperdicio o desecho, residuo o material no deseado o inservible.

La basura es generada por el hombre como consecuencia de sus múltiples actividades relacionadas fundamentalmente con la producción y el consumo. Está constituida por todos aquellos residuos o materiales que ya no son aprovechables o que han perdido su utilidad.

¿Como se clasifica la basura?

La basura la podemos clasificar según su composición que tenga, por ejemplo; en residuos orgánicos, residuos inorgánicos y residuos peligrosos... 

Residuos orgánicos;

Es todo desecho de origen biológico, que alguna vez estuvo vivo o fue parte de un ser vivo , por ejemplo: hojas, rama, cascaras y residuos de la fabricación de alimentos en el hogar, etc.

Residuos inorgánicos;
Es todo desecho de origen no biológico, de origen industrial o de algún otro proceso no natural, por ejemplo: plástico, telas sintéticas, botellas de vidrio, hule, etc.


Residuos peligrosos;
Es todo desecho, ya sea de origen biológico o no, que constituye un peligro potencial y por lo cual debe ser tratado de forma especial, por ejemplo: material medico infeccioso, residuo radiactivo, ácidos y sustancias químicas corrosivas, etc.

"Ejemplos de basura inorgánica y el tiempo aproximado de su desintegración"

*Papel: se compone básicamente de celulosa, por lo que tarda menos de 1 año en formar parte del suelo. No obstante, si no se recicla, contribuyes a que se continúen talando árboles para su fabricación.                                                                                                                                                                                                                    *Las colillas: tardan entre 1 y 2 años en degradarse. Los filtros están hechos de acetato de celulosa y las bacterias del suelo no pueden descomponerlo adecuadamente.                                                                                                                               *Los pañales: tardan de 300 a 400 años en descomponerse.Al contener materiales derivados del petróleo, como polipropileno, polietileno, elásticos, adhesivos y plásticos resultan altamente contaminantes.                                                                                                                                                                                                                   

*Las botellas de plástico: que en su mayoría están hechas de tereftalato de polietileno (PET), un material difícil de degradarse, tardan de 100 a 1.000 años en descomponerse.  Además, si están enterradas tardan más tiempo.

 *Las pilas: tardan de 500 a 1.000 años en descomponerse totalmente. Además, son altamente contaminantes para el medio ambiente, debido a su contenido químico compuesto de materiales como el mercurio.                                                                                                                                                                                                                *Por último, las botellas de vidrio tardan unos 4.000 años en degradarse.

¿Qué problema provoca en los ecosistemas el exceso de basura?

• El consumo de energía y materiales que se utilizan para elaborar envases y productos que después desechamos. Esta energía y estos materiales con frecuencia provienen de recursos que no son renovables, por ejemplo del petróleo y de minerales. 

• La contaminación del agua. El agua superficial se contamina por la basura que tiramos en ríos y cañerías. En los lugares donde se concentra basura se filtran líquidos, conocidos como lixiviados, que contaminan el agua del subsuelo de la que, en nuestra ciudad, todos dependemos.

• La contaminación del suelo, la presencia de aceites, grasas, metales pesados y ácidos, entre otros residuos contaminantes, altera las propiedades físicas, químicas y de fertilidad de los suelos.

• La contaminación del aire, los residuos sólidos abandonados en los basureros a cielo abierto deterioran la calidad del aire que respiramos, a causa de las quemas y los humos, que reducen la visibilidad, y del polvo que levanta el viento en los periodos secos, ya que puede transportar a otros lugares microorganismos nocivos que producen infecciones respiratorias.

"Acerca del problema"

En mi familia vivimos 11 personas y como las demás personas también generamos basura ya sea orgánica o inorgánica, por ejemplo: en la basura orgánica generamos cáscaras de frutas, residuos de verduras, cáscaras de huevo, etc, y en la basura inorgánica se generan por ejemplo: cajas de leche, pedazos de cartón, se desechan bolsas de plástico y comúnmente hojas de papel.

A lo largo del tiempo me eh dado cuenta que en los días en donde se genera más basura es en los días sábado y domingo, ya que en esos días es donde más consumimos más alimentos. 

Aproximadamente cada miembro de mi familia genera 150 gr de basura ya sea orgánica o inorgánica, por lo que diariamente se genera 1.650 kg de basura por todos los integrantes, a la semana se genera al rededor de los 11.550 kg de basura, bimensual 80.85 kg de basura, trimestral 161.7 kg de basura, semestral 485.1 kg de basura y anual 970.2 kg de basura. 

"El problema y su relación matemática"

Haciendo uso de la interpretación de lenguaje algebraico a partir del lenguaje común. Considera la cantidad de kg de basura orgánica con la letra "x", y la cantidad de kg de basura inorgánica con la letra "y".

LENGUAJE VERBAL	LENGUAJE ALGEBRAICO
1.El doble de la cantidad de kg de basura orgánica.	[2x]
2.El triple de la cantidad de kg de basura inorgánica.	[3y]
3.La cantidad de la basura orgánica sobre 2.	x/2
4.Un tercio de la cantidad de kg de la basura inorgánica.	y/3
5.El doble de la cantidad de kg de basura orgánica más 4 kg.	2x + 4
6.El triple de la cantidad de kg de basura inorgánica menos 7 kg.	3y - 7
7.La cantidad de kg de basura orgánica e inorgánica.	X + y
8.El doble de la cantidad de kg de basura orgánica junto con triple de la cantidad de kg de basura inorgánica.	2x + 3y
9.La mitad de la cantidad de kg de basura orgánica menos un tercio de la cantidad de kg de basura inorgánica.	x/2 - y/3

"Responde las siguientes preguntas"..

1.Si la cantidad de basura que genera tu familia, de tipo orgánica es de 20 kg a la semana, ¿Cuál seria su doble?

R= 20 kg 2x = 40 kg 

2. Si la cantidad de kg de basura inorgánica generada en tu hogar es de 25, ¿Cuánto es 3y?

R=  3 x 25 kg = 75 kg

3.Si la cantidad de kg de basura orgánica es 63, ¿Cuál es su doble mas 15 kg?

R= 63 kg x 2 = 126 kg + 15 kg = 141 kg

4.Si x=16 kg  y  y=24 kg, ¿Cuánto es x/2 - y/3=?

R= 16 kg/2 - 24 kg/3 =

       8 kg - 8 kg = 0 kg

5.Si x= 3 kg, entonces el doble de la cantidad de basura orgánica -4 kg = 2 kg, ¿Por qué?

R= 3 kg x 2 = 6 kg      6 kg - 4 kg = 2 

El resultado es igual y da el resultado dado en el problema anterior.

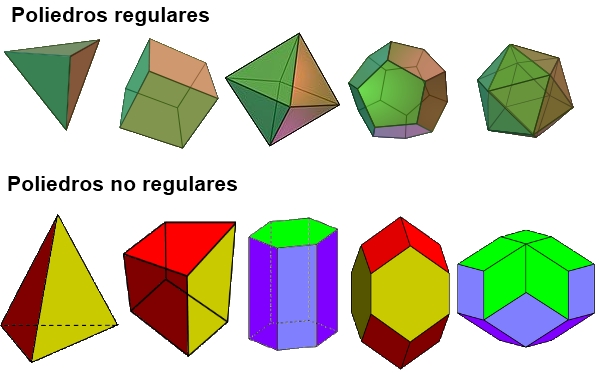
"¿Qué es un poliedro?"

Un poliedro es una figura por polígonos regulares. Los polígonos se utilizan para construir figuras de tres dimensiones llamadas poliedros, que son figuras hechas con cara de polígonos, por ejemplo un cubo esta hecho en base a caras que son cuadradas.

"Características de los poliedros regulares e irregulares"

La clasificación mas importante es en regulares e irregulares. Recordando que los polígonos regulares son de los cuales sus ángulos y lados son congruente, así los poliedros  regulares cumplen con la siguiente característica:

A) Todas las caras son iguales o las mismas.

B) Todas las caras son polígonos regulares.

C) El mismo numero de caras se une a cada vértice.

D) La figura no tiene aberturas ni agujeros.

E) La figura es conversa.

Algunos ejemplo de polígonos regulares son; el cuadrado, el hexágono, el trapecio, etc.

Las características de los polígonos irregulares son;

A) Tienen una base que puede ser un polígono de cualquier forma.

B) Las caras laterales tienen un punto en común llamado vértice.

C) La altura es la medida del segmento perpendicular a las base que pasa por el vértice.

D) Las aristas laterales son las que concurren en el vértice.

E) Las aristas básicas son las que forman la base.

"¿QUÉ ES EL VOLUMEN EN UN POLIEDRO?"

Todos los vértices de un poliedro regular equidistan de un punto interior llamado centro. Haciendo pasar planos por este punto y por todas las aristas, el poliedro queda descompuesto en tantas pirámides iguales como caras tiene. Para calcular el volumen de un poliedro será suficiente calcular el volumen de una de estas pirámides y multiplicar por el número de caras del poliedro.

El volumen de una pirámide es , siendo B el área de la base y "ap" la distancia del centro del poliedro al centro de la cara, distancia que se llama apotema. Siendo N el número de caras , pero  (área total del poliedro), y en consecuencia .

Por lo que a continuación les presento una tabla donde pueden observar como sacarle el volumen a diferentes poliedros regulares:

FIGURA	VOLUMEN
Tetraedro	V= Ab x h/ 3
Cubo	V= a3
Octaedro	V= Ab x h x 2/3
Dodecaedro	V=  1/4 (15+7{5)a3
Icosaedro	V= 5/12 (3+{5)A3
Prisma (cualquiera)	V= Ab (h)
Pirámide (cualquiera)	V= 1/3 Ab (h)

"Ejercicios"

En el municipio de Xiutetelco existe un centro ceremonial prehispánico el cual resulta ser atractivo para diferentes turistas de la región debido a la forma de sus pirámides.

Un turista de San Salvador Xiutetelco quiso determinar el volumen de cada una de ellas para la pirámide mayor se tiene: una base cuadrada de 127 m y una altura de 139 m, para la segunda pirámide igual con una base cuadrada de 119 m y una altura de 121 m, y para la tercera pirámide  cuya base mide 98 m y su altura de 111 m. Cual es el proceso de solución que utilizo este turista de San Salvador Xiutetelco para determinar el volumen de cada una de ellas...

"La importancia de sacar un volumen de un poliedro"

El sacar el volumen de un poliedro es muy importante, ya que al tener las funciones de como sacar el volumen de diferentes poliedros se te va hacer fácil sacarlos. Por ejemplo cuan vas a visitar las pirámides de algún lugar vas a pensar de como se puede sacar el volumen de estas grandes arquitecturas, entonces recordaras estas funciones y las vas hacer para saber cual es el volumen de las pirámides .

Por lo que al tener y saber cuales son las funciones se te hará mas fácil sacarles, por lo que es importante conocer las funciones de los poliedros para que en futuro se te haga mas  fácil  resolver los problemas de poliedros y poder sacar su volumen de cualquier poliedro.  

"TRABAJOS Y TAREAS SEMANALES"

 

Semana 1...

Semana 2
 

Semana 3

Semana 4

"PLANO CARTESIANO"

Las coordenadas cartesianas o coordenadas rectangulares (sistema cartesiano) son un tipo de coordenadas ortogonales usadas en espacios euclídeos, para la representación gráfica de una relación matemática (funciones matemáticas y ecuaciones de geometría analítica), o del movimiento o posición en física, caracterizadas por tener como referencia ejes ortogonales entre sí que concurren en el punto origen. En las coordenadas cartesianas se determinan las coordenadas al origen como la longitud de cada una de las proyecciones ortogonales de un punto dado sobre cada uno de los ejes. La denominación de 'cartesiano' se introdujo en honor de René Descartes, quien las utilizó por primera vez de manera formal.

El sistema en sí es un sistema bidimensional, que se denomina plano cartesiano. El punto de intersección de las rectas, por definición, considera como el punto cero de las rectas y se conoce como origen de coordenadas. Al eje horizontal o de las abscisas se le asigna los números reales de las equis ("x"); y al eje vertical o de las ordenadas se le asignan los números reales de las yes ("y").

 

 

 Semana 5

 

 

Semana 6

 

Semana 7 

"Plano cartesiano"

 

 

 

"Punto medio"

 

"Línea recta"

Semana 8

Cuando los puntos se encuentran ubicados sobre el eje x o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas.
Ejemplo: La distancia entre los puntos (-4,0) y (5,0) es 4 + 5 = 9 unidades.
Cuando los puntos se encuentran ubicados sobre el eje y o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas.
Ahora si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación:

Para demostrar esta relación se deben ubicar los puntos A(x1,y1) y B(x2,y2) en el sistema de coordenadas, luego formar un triángulo rectángulo de hipotenusa AB y emplear el teorema de Pitágoras.  

Puntos medios del mapa...

Sonora (-7.5, 4.5)

Sinaloa (-4.5, 0.5)        Pm: -6, 2.5

B. California (-11, 7)

Chihuahua (-3, 4)         Pm: -7, 5.5

B. California Sur (-8,1)

Coahuila (-1,3)             Pm: -4.5, 2

Durango (-2.5,1)

Jalisco (-1.5,-3.5)         Pm: -2, 1.5

Zacatecas (-1,-1)

Guanajuato (1,-3)         Pm: 0, -2

Colima (-2,-4.5)

Guerrero (2,-6)             Pm: 0, -5.2

Puebla (3,-5)

Oaxaca (4,-6.5)            Pm: 3.5, -5.7

Querétaro (2,-3)

Veracruz (5,-5)             Pm: 3.5, -4

Campeche (10,-4)

Chiapas (8,-7)              Pm: 9, -5.5

Nuevo León (1,2)

Yucatán (11,-3)            Pm: 6, -0.5

Reflexión...

El punto medio , es el punto que se encuentra a la misma distancia de cualquiera otros dos puntos o extremos de un segmento. Generalmente es el punto que se encuentra a la misma distancia de dos elementos geométricos, ya sean puntos, segmentos, rectas, etc.

Si es un segmento, el punto medio es el que lo divide en dos partes iguales. En ese caso, el punto medio es único y equidista de los extremos del segmento. Por cumplir esta última condición, pertenece a la mediatriz del segmento.

Se hace buscando puntos del eje de simetría de los elementos dados en cada caso. Si no son simétricos se hacen aproximaciones mediante arcos o paralelas para hallar los puntos medios o equidistantes según el caso. Por lo que es importante conocer cual es la distancia entre dos puntos y el punto medio de cualquier segmento que adquiera...



Semana 9

"Producto notable"

Se le llama identidad notable o producto notable a un cierto producto que cumple reglas fijas y cuyo resultado puede ser escrito por simple inspección, es decir, sin verificar la multiplicación.

Cada producto notable corresponde a una fórmula de factorización. Por ejemplo, la factorización de una diferencia de cuadrados perfectos es un producto de dos binomios conjugados

Aplicaciones...

Cada producto notable corresponde a una fórmula de factorización. Por ejemplo, la factorización de una diferencia de cuadrados perfectos es un producto de dos binomios conjugados, y recíprocamente.

 Factor común

Representación gráfica de la regla de factor común.

El resultado de multiplicar un binomio a+b por un término c se obtiene aplicando la propiedad distributiva:

Para esta operación existe una interpretación geométrica, ilustrada en la figura adjunta. El área del rectángulo es

 (el producto de la base por la altura), que también puede obtenerse como la suma de las dos áreas coloreadas: ca y cb.

Ejemplo:

Binomio al cuadrado o cuadrado de un binomio

Ilustración gráfica del binomio al cuadrado.

Para elevar un binomio al cuadrado (es decir, multiplicarlo por sí mismo), se suman los cuadrados de cada término con el doble del producto de ellos. Así:

Un trinomio de la expresión siguiente:  se conoce como trinomio cuadrado perfecto.
Cuando el segundo término es negativo, la ecuación que se obtiene es:

En ambos casos el signo del tercer término es siempre positivo.
Ejemplo:

Simplificando:

Producto de dos binomios con un término común

Ilustración gráfica del producto de binomios con un término común.

Cuando se multiplican dos binomios que tienen un término común, el cuadrado del término común se suma con el producto del término común por la suma de los otros, y al resultado se añade el producto de los términos diferentes.

Ejemplo:

Agrupando términos:

Luego:

Producto de dos binomios conjugados

Véase también: Conjugado (matemática).

Producto de binomios conjugados.

Dos binomios conjugados se diferencian sólo en el signo de la operación. Para su multiplicación basta elevar los monomios al cuadrado y restarlos (obviamente, un término conserva el signo negativo), con lo cual se obtiene una diferencia de cuadrados.

Ejemplo:

Agrupando términos:

A este producto notable también se le conoce como suma por la diferencia.

Polinomio al cuadrado

Elevación de un trinomio al cuadrado de forma gráfica.

Para elevar un polinomio de cualquier cantidad de términos se suman los cuadrados de cada término individual y luego se añade el doble de la suma de los productos de cada posible par de términos.

Ejemplo:

Multiplicando los monomios:

Agrupando términos:

Luego:

Binomio al cubo o cubo de un binomio

Para calcular el cubo de un binomio se suman, sucesivamente:

• El cubo del primer término con el triple producto del cuadrado del primero por el segundo.
• El triple producto del primero por el cuadrado del segundo.
• El cubo del segundo término.

Reglas...

1. Cuadrado de la suma de dos cantidades

Cuando tenemos dos cantidades a y b, cuya suma está elevada al cuadrado, lo que realmente se pide es que se multiplique la suma por si misma:

Esta multiplicación se efectúa de la siguiente forma:

Regla del cuadrado de la suma de dos cantidades

El cuadrado de la suma de dos cantidades es igual al cuadrado de la primera cantidad, más dos veces la primera cantidad por la segunda, más el cuadrado de la segunda cantidad.

Representación gráfica del cuadrado de la suma de dos cantidades

El cuadrado de la suma de a y b se representa como un cuadrado compuesto por los cuadrados de a y de b y dos rectángulos cuyos lados son a y b.

Podemos representar gráficamente el cuadrado de la suma de dos cantidades cuando los valores son positivos. Así, la suma de dos cantidades positivas al cuadrado será igual a la suma de:

• un cuadrado con sus lados iguales a la primera cantidad;
• un cuadrado con sus lados iguales a la segunda cantidad, y
• dos rectángulos cuyos lados son iguales a la primera y la segundad cantidad.

Como podemos ver, el cuadrado resultante tendrá un área igual a (a+b) por (a+b)= (a+b)²

Ejemplos con solución paso a paso

1) Desarrolle (x+10)².

• Cuadrado del primer término: x².
• Dos veces el primero por el segundo: 2(x)(10)=20x.
• Cuadrado del segundo término: 10²=100.

Respuesta:

2) Desarrolle (7a²+5x³)².

• Cuadrado del primer término: 7²(a²)²=49a⁴.
• Dos veces el primero por el segundo: 2(7a²)(5x³)= 70a²x³.
• Cuadrado del segundo término: (5)²(x³)²=25x⁶.

Respuesta:

2. Cuadrado de la diferencia de dos cantidades

Cuando tenemos dos cantidades a y b, cuya resta está elevada al cuadrado, lo que realmente se pide es que se multiplique la resta por si misma:

Esta multiplicación se efectúa de la siguiente forma:

Recordemos que dos números negativos cuando se multiplican, el signo resultante es positivo:

Características...

• Posee internamente la suma de dos términos.

• Esta suma esta elevada a una potencia.

• La potencia debe ser un número entero y mayor o igual a  2

• Pueden ser sumas o restas internas

Reporte...

Las ecuaciones de segundo grado son importantes para cualquier solución de  problema, ya sean matemáticos o de otra materia. 

 En cualquier problema matemáticos de ecuaciones de segundo grado, se necesitan este tipo de ecuaciones para mostrar darles una solución, de igual modo se puede utilizar en la vida diaria, ya sea cuando se construye una casa se necesita saber las medidas,  los metros de algún terreno que se quiere medir, etc...

Las ecuaciones de segundo grado también son útiles para cualquier problema, donde se requiera el uso de problemas matemáticos...

Semana 10

Sistemas de dos ecuaciones lineales con dos incógnitas...

Los sistemas de ecuaciones lineales de 2 x 2 (llamados comúnmente como sistemas de ecuaciones de 2x2 o sistemas de 2 x 2) se pueden resolver por varios métodos:

• Método gráfico
• Sustitución
• Eliminación
• Igualación

A continuación encontrarás algunos ejemplos resueltos paso a paso de cómo resolver sistemas de dos ecuaciones  lineales con dos incógnitas por el método de suma y resta.

Ejemplo 

Resolveremos este sistema de ecuaciones por el método de eliminación:

${\displaystyle 6x-y=1}$

Observa que la variable Y aparece en ambas ecuaciones con signo opuesto, y que además está acompañada por el mismo número en ambas ecuaciones: en ambas está acompañada por un 1. Debido a esto, si sumamos ambas ecuaciones, el término Ydesaparecerá.

${\displaystyle {\begin{alignedat}{2}4x+y=9\\{\underline {+\quad 6x-y=1}}\\10x=10\end{alignedat}}}$

Obtuvimos la ecuación 10X = 10, que podemos despejar fácilmente:

${\displaystyle {\begin{alignedat}{2}10x=10\\x={\frac {10}{10}}\\x=1\end{alignedat}}}$

Así que X = 1. Ahora, podemos reemplazar ese valor de X en cualquiera de las dos ecuaciones que teníamos inicialmente, y despejar Y:

${\displaystyle {\begin{alignedat}{2}4x+y=9\\4*1+y=9\\4+y=9\\y=9-4\\y=5\end{alignedat}}}$

Y listo. Tenemos la solución al sistema de ecuaciones:

${\displaystyle {\begin{alignedat}{2}x=1\\y=5\end{alignedat}}}$

Ejemplo 2

Vamos a resolver el siguiente sistema de ecuaciones por el método de eliminación:

PASO 1

Ordenamos ambas ecuaciones, de modo que X y Y aparezcan en el mismo orden en ambas.

${\displaystyle {\begin{alignedat}{2}2x+y=8\\3x+4y=17\end{alignedat}}}$

PASO 2

Debemos decidir cuál variable vamos a eliminar. En este caso, eliminaremos la Y. Para eliminarla, necesitamos que esté en ambas ecuaciones acompañada por el mismo coeficiente, pero con signos opuestos (es decir, necesitamos que en una ecuación aparezca con signo positivo y en la otra con signo negativo)

PASO 3

Multiplicamos cada ecuación por el coeficiente que acompañe a Y en la otraecuación.

En este caso, observa que en la primera ecuación la Y está acompañada por un 1, mientras que en la segunda está acompañada por un 4, así que deberíamos multiplicar la primera ecuación por el 4 y la segunda ecuación por el 1. Sin embargo, necesitamos que una de las dos Y sea negativa, así que vamos a multiplicar la segunda ecuación por -1.

${\displaystyle {\begin{alignedat}{2}(2x+y=8)\cdot 4\qquad \rightarrow \qquad 8x+4y=32\\(3x+4y=17)\cdot -1\quad \rightarrow \ -3x-4y=-17\end{alignedat}}}$

PASO 4

Sumamos ambas ecuaciones.

${\displaystyle {\begin{alignedat}{2}8x+4y=32\\{\underline {+\quad -3x-4y=-17}}\\5x=15\end{alignedat}}}$

PASO 5

Despejamos la variable que queda.

${\displaystyle {\begin{alignedat}{2}5x=15\\x={\frac {15}{5}}=3\end{alignedat}}}$

PASO 6

Ya tenemos una variable despejada. Ahora la reemplazamos en cualquiera de las dos ecuaciones que teníamos inicialmente, y despejamos la otra variable

${\displaystyle {\begin{alignedat}{2}y+2x=8\\y+2\cdot 3=8\\y+6=8\\y=8-6\\y=2\end{alignedat}}}$

Y ya está resuelto el sistema de ecuaciones:

${\displaystyle {\begin{alignedat}{2}x=3\\y=2\end{alignedat}}}$